CT – Optimalt mätverktyg för medicinska produkter.

Medicinska produkter har ofta tuffa kvalitetskrav vilket kräver att mätutrustningen inte bara måste kunna mäta noggrant utan även kunna mäta dolda mått inuti produkterna. Oftast är de produkter som skall mätas av plast eller annat mjukt material vilket inte tål en fysisk probmätning. Likaså kräver en mätning med ett optiskt system att plastytor behandlas med en spray före en mätning för att vara säker på att mätningen sker på ytan och inte en bit in i plasten.

Det optimala mätverktyget för medicinska produkter är en CT-scanner som klarar av mätning med hög noggrannhet.

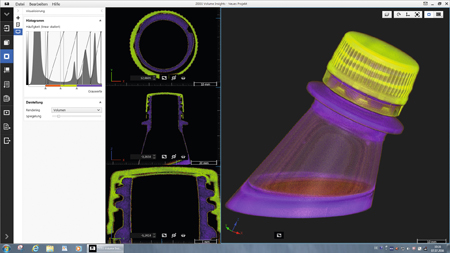
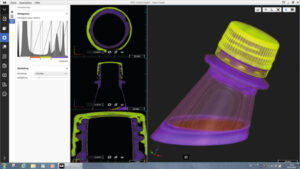
En CT-scanner kan även användas för att ta reda på dolda hålrum i ett objekt eller porositet. Med programvaran ZEISS INSPECT X-RAY går det att få reda på var porositeten finns, hur mycket och hur många porer/hålrum är större än ett visst mått.

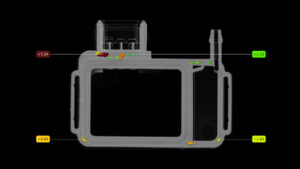
En annan mätteknisk svår uppgift är att ta reda på hur bra två eller fler sammanfogade objekt passar mot varandra. Att kunna få se en dold sampassning plus få mått på hur bra sampassningen är uppskattas stort av de som använt CT-data för detta ändamål.

Med en CT från ZEISS kan man även mäta många detaljer samtidigt vilket ger en ytterst kort mättid per enskild detalj. Detaljerna placeras i cellplast som fungerar som en enkel och snabbskapad fixtur. Storleken på detaljerna som skall mätas styr hur många som kan mätas samtidigt. Att mäta 50 st små objekt samtidigt är ingen omöjlighet. Efter att mätningen har skett kan programvaran ZEISS INSPECT X-RAY dela upp mängden föremål och ge en resultatrapport för varje enskild detalj. Resultatrapporten kan innehålla form & lägesanalyser, längdmått, volym osv.

Vi på Cascade har kontrollerat kvaliteten på medicinska produkter i många år och kan därför hjälpa till med mätning med en ZEISS-CT eller finna rätt mätverktyg för era medicinska produkter. Ta gärna kontakt med oss via info@cascade.se